variable dependent processes

Hello,

Can logical switches be used in "Constants and Expressions" to make processes dynamically dependent on a model variable in space and time?  I am modeling reactive transport in which one substance (A) undergoes first order decay at a rate k until its substrate (B) is depleted (so k = 0 if B = 0).  I tried implementing this by defining the convection/diffusion source term "R" in "Constants and Expressions" as:
R = -k*A*(B>0).

However, it appears that FEAtool is not enforcing the logical switch during the simulation.  The reaction continues even after B is depleted.

My assumption is that FEAtool evaluates R at each node at each time, such that:
R(x,y,t) = -k*A(x,y,t)*(B(x,y,t)>0)

Is my understanding correct?  Any issues in my syntax?

Thanks!

Yes, switch expressions either evaluate to 0 or 1 depending on the expression. You could try to plot the expression in postprocessing mode for different time steps to see the value. Also note that it will be discontinuous in space (some regions might evaluate to 1 and others to 0). If this is an issue one can also try to implement smooth Heaviside functions according to the thesis of A.-K. Tornberg, Interface Tracking Methods with Application to Multi-phase Flows, PhD Thesis, NADA, KTH, Stockholm, Sweden, 2000, ISBN: 91-7170-558-9, TRITA-NA 0010.

Another potential source of negative values of convection-diffusion equations might be due to the numerical scheme which isn't by default monotonicity preserving (positive initial conditions do not ensure positive results over time). To ensue this a (FEM-)TVD stabilization scheme must be used by selecting Shock Capturing from the Artificial Stabilization dialog box https://featool.com/doc/physics#phys_artstab .

If the issues remain, please attach model or example file if possible to more precisely diagnose the issue (it could of course potentially be a bug as well).

Thanks for the response.

I have a few of related questions on how equations are coded in the GUI interface.


(1) The GUI’s description for convection/diffusion of A is: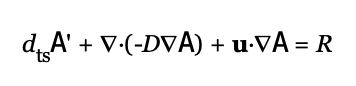
 

When I click “edit”, FEAtool shows this:
dts_cd3*A' - d_cd3*(Ax_x + Ay_y + Az_z) + (u_cd3*Ax_t + v_cd3*Ay_t + w_cd3*Az_t) = r_cd3

The above forms don’t seem to match…is it actually solving the spatially constant D case shown below?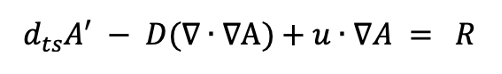


If it is, how would I write the spatially variable isotropic diffusion case D(x,y) using FEAtool shorthand derivative notation?  Something like this?
dts_cd3*A' - d_cd3*(Ax_x + Ay_y + Az_z) - (Ax*d_cd3x + Ay*d_cd3y + Az*d_cd3z) + (u_cd3*Ax_t + v_cd3*Ay_t + w_cd3*Az_t) = r_cd3


(2) Let’s say I wanted to model the diffusion (setting u = v = w = 0) of a new quantity A*G where G is a spatially variable parameter that varies by subdomain but not within a subdomain.  Per your prior responses, my understanding is that I can specify subdomain variability using G = [G1 G2] via "Constants and Expressions" for the case of two subdomains.  Can I model the product (AG) directly using the FEAtool shorthand derivative notation or do I need to expand the terms to separate A and G?


(3) In general, my understanding of the FEAtool shorthand notation from the brief documentation and the equation above is that A’ means dA/dt, Ax means dA/dx and Ax_x means d(dA/dx)/dx.  Is that correct?  If so, what does Ax_t mean, which also appears in the above equation?  The prior syntax suggests Ax_t means d(dA/dx)/dt, but that doesn’t make any sense given the governing equation so I suspect I am misinterpreting the convention.

Thanks.

(1)

The underscore "_x" form in "D*Ax_x" implies partial integration (via the Galerkin finite element method, int_Omega(D*dA/dx*dv/dx) where v is a test function. The form "D*Axx" would be equivalent to your second example (although not recommended if it even works). However, if the diffusion coefficient "D" is constant they are equivalent.

(2)

Could you clarify how G varies with time and space? If G is just a constant varying with the subdomain it should work as expected, but if it is more complicated it could possibly be that the implicitly induced (Neumann) boundary conditions between the subdomains might cause negative values of your dependent variable A.

(3)

Although maybe a little hidden, the equation syntax is specified here https://featool.com/doc/physics#phys_ce

So the form "#_t" indicates the # is multiplied with a test function. So for example the difference between "Ax" and "Ax_t" will be that "Ax" is assembled on the RHS (load vector, as dA/dx) and "Ax_t" is a bilinear form assembled to the stiffness matrix (dA/dx*v where v is a test function) which usually is more computationally efficient for linear terms, but also has bearing on if a term will appear in the Neumann boundary conditions (everything with underscore _).

Thanks for the clarifications and sorry for my slow reply.

(1)  OK that makes better sense.   So from your explanation FEAtool is indeed solving the case of a spatially variable D.  That's reassuring to hear!


(2) Regarding your question under (2), yes G is just a constant within each subdomain but different between subdomains.


(3) Thanks for showing me where the syntax description is.

So based on my understanding, if I want to model this equation where A is the concentration and G is a parameter that varies by subdomain (spatially uniform within each subdomain and constant in time):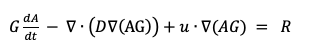


...then the FEAtool equivalent is this:
dts_cd*G*A' - d_cd*(G*Ax_x + G*Ay_y + G*Az_z) + (u_cd*G*Ax_t + v_cd*G*Ay_t + w_cd*G*Az_t) = r_cd

Do I have the syntax right?


Thanks!

Peter

I believe this should be sufficient:

    dts_cd*G*A' - d_cd*G*(Ax_x +*Ay_y + Az_z) + G*(u_cd*Ax_t + v_cd*Ay_t + w_cd*Az_t) = r_cd

and if you actually don't have convective terms you can of course omit those as well.

Thank you for confirming.