Syntax for "Flux Discontinuity" boundary condition at internal boundaries

Hello,

I am modeling convection/diffusion for two subdomains with a diffusion coefficient that varies by several orders of magnitude between the subdomains, but is constant within each subdomain.  FEAtool seems to have trouble with the numerics of this discontinuity and I'm getting negative concentrations which build over time.  It's not due to the advective term because u = 0 everywhere.

I am thinking that a practical way around this (while avoiding coefficient smoothing zones and small timesteps) would be to use the "Flux discontinuity" option at the internal boundaries between the subdomains.  I've reviewed a past thread on this general topic here, which had a helpful figure:


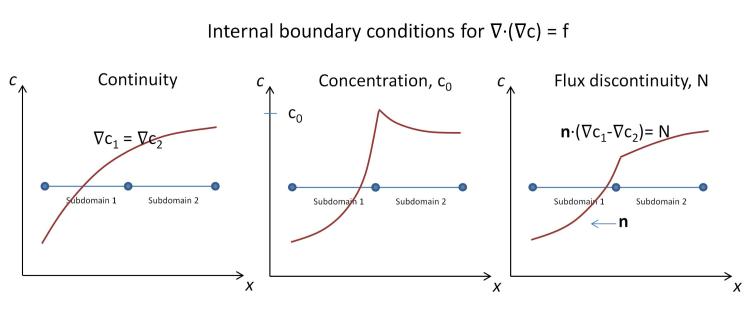
I'd like to use an analytical solution to specify the net flux between the domains, specified as an equation at the internal boundaries in the "N_0" field below.  Is that possible?



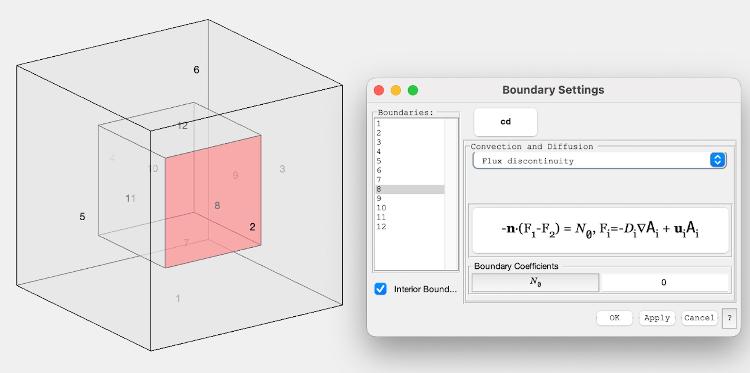
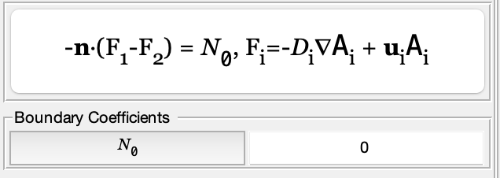
To do this, I will need to be able to reference the concentration of solute A on either side of the boundary (i.e., A at x-  and x+ or  y- and y+  or  z- and z+, depending on the orientation of the boundary) and ideally also the diffusion coefficients on either side (although that's less critical because they are known inputs).  Is there a way to do that in FEAtool's syntax?

I've reviewed the syntax documentation previously shared (here) but I don't see anything on this.

Thanks!
Peter

peteri wrote

FEAtool seems to have trouble with the numerics of this discontinuity and I'm getting negative concentrations which build over time.

This is quite likely due to the Galerkin finite element method which assumes C1 continuity in the test function and solution spaces. There are other formulations as well such as "discontinous Galerkin" however this formulation is not supported by FEATool. An alternative, as hinted at earlier is to use a smoothed heaviside function (a.la. Tornbergs thesis)  with the drawback is that the transition won't be sharp anymore.

 

I'd like to use an analytical solution to specify the net flux between the domains, specified as an equation at the internal boundaries in the "N_0" field below.  Is that possible?

To do this, I will need to be able to reference the concentration of solute A on either side of the boundary (i.e., A at x-  and x+ or  y- and y+  or  z- and z+, depending on the orientation of the boundary) and ideally also the diffusion coefficients on either side (although that's less critical because they are known inputs).  Is there a way to do that in FEAtool's syntax?

The standard evaluation of boundary conditions just evaluates it at the actual boundary. The normal is defined as pointing from the region with higher subdomain number to lower, but there is no "side" for evaluating variables as they are evaluated on the boundary itself. In the FEM formulation with continuous elements your variable A will not have a difference between the sides (on the boundary itself). You could possibly create a custom function to compute the flux how you like, but I'm not sure how well it would work anyway. Some example how to construct custom boundary evaluations can be found in the examples for periodic boundary conditions:

https://www.featool.com/tutorial/2017/10/30/Periodic-Boundary-Conditions-and-the-Solver-Hook-Functionality

Also, some example using smoothed Heaviside functions for multiphase flow with the level set method can be found in the corresponding m-file examples:

https://featool.com/doc/ex__multiphase1_8m
https://featool.com/doc/ex__multiphase2_8m
https://featool.com/doc/ex__multiphase3_8m