Modeling DC conduction electrodes using Point vs. Sphere objects
|
This question falls out from the "Basic Use" forum post "Setting boundary conditions for point sources".
http://forum.featool.com/Setting-boundary-conditions-for-point-sources-tp965p967.html : I have made a few attempts. In the latest one I added a boundary plane in the middle and between the electrodes to measure total current, but my results indicate that I am missing something. The 'XY' plane iso line plots are very different as is the total current: Here is the point source version with 120V at P1 and 0V at P2: pointBoundaryConstraintSplit.fea 'XY' slice plot containing (0,0,0): 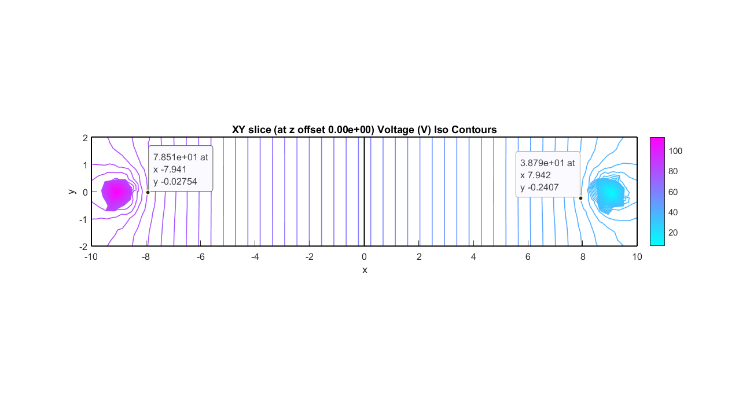 Integration of expression '-s_dc*(nx*Vx+ny*Vy+nz*Vz)' on boundary 11 : 0.19064 And here is the Spherical electrode version: splericalElectrodesSplit.fea And 'XY' plot: 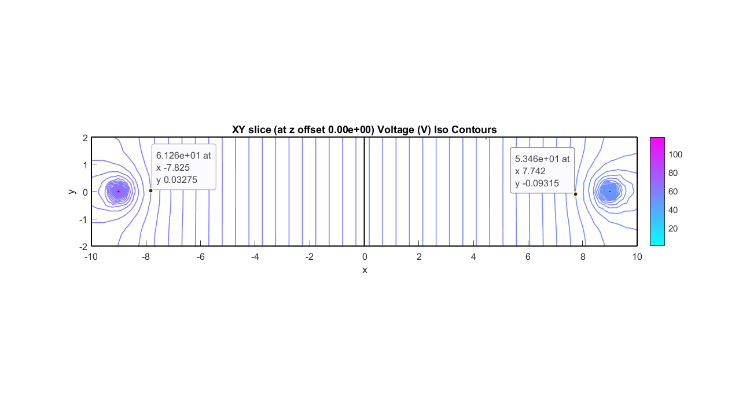 Integration of expression '-s_dc*(nx*Vx+ny*Vy+nz*Vz)' on boundary 27 : 0.038615 On the one hand, it is obvious that a point and a sphere are entirely different "animals" - one has only location while the other has location and 3 spatial dimensions. And a the current density near a point electrode increases without bounds the nearer it is considered. On the other hand, it would seem that, while one cannot construct a point electrode in the real world, as a spherical electrode gets smaller and smaller it might be expected to give the results that closer and closer approximates that of a theoretical point. For my particular use case: conduction of electricity in water, modeling a 3 dimensional object would almost always be preferred. However, I can imagine that for large bodies of water that relatively very small electrodes might present geometry problems which could possibly be eliminated by using point electrodes. Can, and if so how can, point objects be used to model 3 dimensional objects in a DC conduction FEA model? Thank you and kind regards, Randal |
Re: Modeling DC conduction electrodes using Point vs. Sphere objects
|
Administrator
|
To me it looks like the solutions are roughly the same, the fact that you get slightly different contour plots near the sources I'm guessing is due to that you have a finer grid near the sources in the sphere version.
Basically, to exactly compare simulations you ideally should have identical meshes or as close to as possible. I would therefore expect that both cases would more or less converge when performing mesh convergence studies (comparing solutions on successively uniformly refined grids).
(point)
Mesh | n_p | int(V) | int(ncd)
0 | 4k | 939 | 0.190
1 | 31k | 935 | 0.113
2 | 226k | 932 | 0.062
(sphere)
Mesh | n_p | int(V) | int(ncd)
0 | 5k | 917 | 0.039
1 | 36k | 933 | 0.035
2 | 269k | 939 | 0.033
Also remember that the current density is defined as a gradient of the potential (dependent variable) so will not be as accurate. Tip: for simple scalar Poisson type problems, such as for electrostatics/conductive media DC the algebraic multigrid (AMG) solver can be significantly more efficient for larger problem sizes. |
I am encouraged that you think these, when done with sufficient "fidelity" (grid), can be made to produce an equivalent E field. But I can see that I will need to wait until I have "beefed" up my processor resources. I have been determining my smallest grid size more based on my computer capabilities rather than what might be needed to get good results. Thanks for getting me started on this. I tightened up the grid for the constrained pointseveral times and got similar results: ---- refined Integration of expression '-s_dc*(nx*Vx+ny*Vy+nz*Vz)' on boundary 11 : 0.11321 Info: - 190925 tetrahedra created in 4.08723 sec. (46712 tets/s) Integration of expression '-s_dc*(nx*Vx+ny*Vy+nz*Vz)' on boundary 11 : 0.10082 Info: - 447661 tetrahedra created in 10.7641 sec. (41588 tets/s t_tot : 9503.8 Integration of expression '-s_dc*(nx*Vx+ny*Vy+nz*Vz)' on boundary 11 : 0.078773 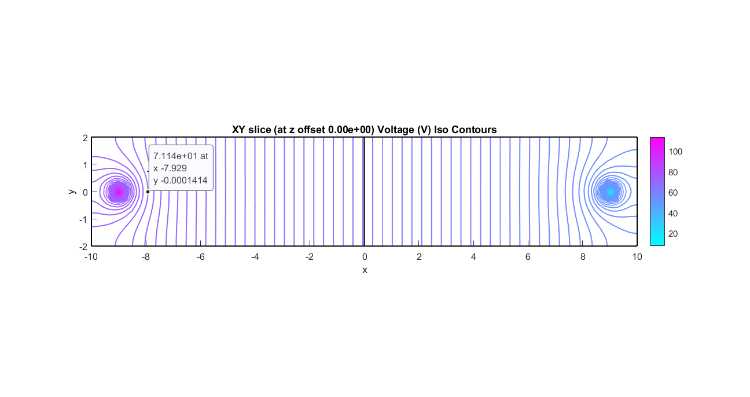 One other thing that concerns me is why the center of the field is not located closer to 0.900. 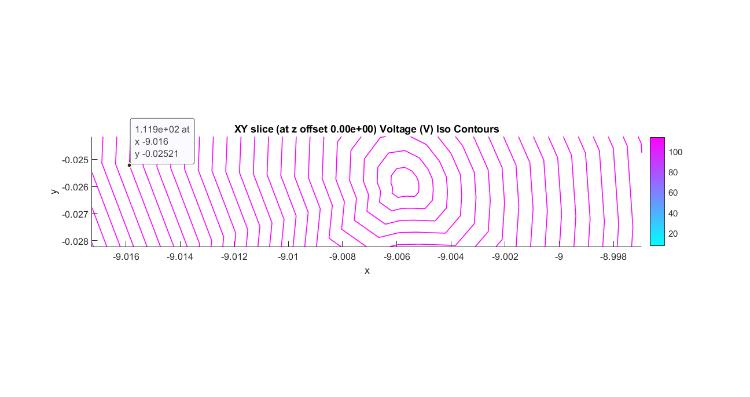 I want to come back to this in a few weeks. I still think there are some things I need to learn from it. Ah.... I'll say!! The final constrained point solution above that took t_tot : 9503.8 (backslash) t_tot : 42.7 (AMG)When should I ever want to use backslash or mumps? In the near future I should be doing nothing besides DC Conduction through media of uniform conductivity. Thanks! and... Kind regards, -Randal |
Re: Modeling DC conduction electrodes using Point vs. Sphere objects
|
Administrator
|
Mumps and UMFPACK/Suitesparse (Matlab's backslash) are very robust direct sparse LU solvers that will work for almost any system but are slow and very memory intense for large systems (requirements scale exponentially). Algebraic multigrid (AMG) and other iterative solvers (GMRES/Bicgstab etc) are very efficient but usually only work robustly on simple Poisson type problems (positive semi-definite systems), and hence are not used as default linear solvers. You can always try if it will work. |
Once I get going with my "FEA" computer, I think I will revisit some past work and compare the solutions using MUMPS and AMG/GMRES/Bicgstab. Thanks again for offering this suggestion ... I had no idea, being the FEA novice that I am :-) Kind regards, -Randal |
Re: Modeling DC conduction electrodes using Point vs. Sphere objects
|
Administrator
|
Possibly you meant comparing the models in general but comparing just linear solvers is not a good use of time, typically either a linear solver converged in which case it doesn't matter which you use as the solutions should be identical (within floating point precision), or you don't get a (meaningful) solution at all. |
What I "meant" (quotes because I am in over my head here :-) ... is to compare "direct sparse LU" solvers, such as MUMPS or backslash, with the iterative solvers, such as GMRES/Bicgstab etc., in solving the problems that I have worked on so far - all conductive DC media. The solver I have used (unless there was an issue) is the default, which, prior to the latest release was MUMPS. And if my problems are in fact "simple scalar Poisson type problems, such as for electrostatics/conductive media DC", then it would seem that my solver of choice should be the AMG or another of the iterative solvers (GMRES/Bicstab). To test this theory, I thought I would go back and run some of my problems using AMG or GMRES/Bicstab and compare solutions (time and results). Hopefully I have written enough here that you might be able to determine what it is that I got wrong, if I am misunderstanding when the iterative should be used over the robust (closed form??). That solution time difference was astounding: over 2 orders of magnitude. (I realize that with more RAM, the MUMPS would have probably been faster than it was, so a proper comparison will have to be done later when I have more memory.) Thanks and kind regards, -Randal |
Re: Modeling DC conduction electrodes using Point vs. Sphere objects
|
Administrator
|
Assuming a linear solver has converged (within a specified tolerance) the resulting solution should be completely independent of method getting there (direct or iterative), only the speed/memory consumption would differ. If its not there is a bug in the (linear) solver. LU decomposition used by direct solvers scale on the order of ~n^3 (with n being the size of the matrix/number of unknowns), where as multigrid solvers scale linearly ~n so there will be magnitudes of difference for large problem sizes. A multigrid solver would always be preferred when it works, however for coupled and non-linear problems it would usually involve elaborate manual construction of the involved matrices which is non-feasible to automate. Again, there is no harm in trying as you either get a correct solution or nothing. Note that this discussion only applies to the lowest level of solving a sparse matrix and linear system. Meshes, discretization options, etc can all lead to more or less different solutions, but the linear solvers should either binary work or not. |
«
Return to Modeling and Simulation
|
1 view|%1 views
| Free forum by Nabble | Edit this page |

