Custom Boundary Conditions and Diffusive Terms

Hello, I have a question regarding the implementation of the following custom slip boundary condition:


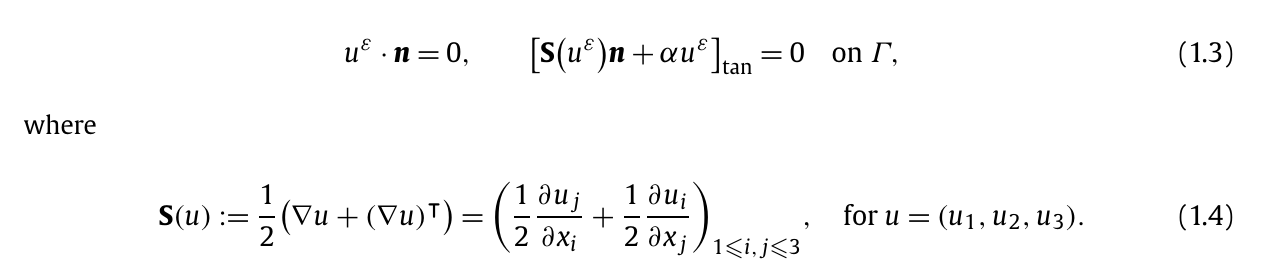This is a slip boundary condition that includes friction, modeled using the alpha parameter. I am considering using a hook function for its implementation. Would this be the correct approach? If so, should I first define the boundary condition arbitrarily in the GUI and then override it with the hook function? I'm unclear about how this process works.

Additionally, I would like to evaluate and visualize the second spatial derivative, ux_x, or related diffusive terms such as the pressure diffusion term, px_x, within the simulation. While I see that it is possible to plot and evaluate the spatial gradient, is there a way to save and plot these higher-order derivatives, particularly along the boundaries of an object in flow?


Thanks, Sean

Sean_Smith wrote

I am considering using a hook function for its implementation. Would this be the correct approach? If so, should I first define the boundary condition arbitrarily in the GUI and then override it with the hook function?

Possibly, you would probably have to introduce extra rows for the slip boundary degrees of freedom (as Lagrange multipliers), assign your slip condition to them, solve, and then remove them again.

Sean_Smith wrote

Additionally, I would like to evaluate and visualize the second spatial derivative, ux_x, or related diffusive terms such as the pressure diffusion term, px_x, within the simulation. While I see that it is possible to plot and evaluate the spatial gradient, is there a way to save and plot these higher-order derivatives, particularly along the boundaries of an object in flow?

The variables "uxx, uxy, uyy" etc. (no underscore) are defined for a subset of finite element types. However, it would not be as accurate as using gradient recovery methods (on the command line).

Are there any examples showing a similar process to:

"Possibly, you would probably have to introduce extra rows for the slip boundary degrees of freedom (as Lagrange multipliers), assign your slip condition to them, solve, and then remove them again."?

Lastly, is it possible to save and export values on curved surface boundaries (such as u \dot n or the normal pressure/pressure gradient etc)?. The documentation mentions how these are calculated:

Normals
Boundary coefficients may use the external normals by prefixing a space dimension name with the character n, as for example nx for the normal in the x-direction. Boundary normals are evaluated and computed as the outward pointing unit vector from the center of each external cell edge or face.

Just curious if these calculations can be saved and plotted.

Sean_Smith wrote

Are there any examples showing a similar process to:

"Possibly, you would probably have to introduce extra rows for the slip boundary degrees of freedom (as Lagrange multipliers), assign your slip condition to them, solve, and then remove them again."?

Not a lot, as it hasn't been a popular feature. This post explains a little

https://www.featool.com/tutorial/2017/10/30/Periodic-Boundary-Conditions-and-the-Solver-Hook-Functionality/

together with these script examples:

https://github.com/precise-simulation/featool-multiphysics/blob/master/examples/ex_periodic1.m
https://github.com/precise-simulation/featool-multiphysics/blob/master/examples/ex_periodic2.m

Sean_Smith wrote

Lastly, is it possible to save and export values on curved surface boundaries (such as u \dot n or the normal pressure/pressure gradient etc)?.

On the Matlab command line you can use the "evalexpr" and "evalexpr0" functions to evaluate expressions on boundaries and subdomains, and then you can manually "save" or plot them with normal Matlab commands.

https://featool.com/doc/evalexpr_8m  (evaluation at arbitrary points)
https://featool.com/doc/evalexpr0_8m  (evaluation in quadrature points)

You can find the evalexpr function used in many of the simulation scripts in the featool examples folder:

ex_axistressstrain1.m:102:6:u  = evalexpr( fea.phys.css.eqn.vars{3,2}, [r;z], fea );
ex_axistressstrain1.m:103:6:w  = evalexpr( fea.phys.css.eqn.vars{4,2}, [r;z], fea );
ex_axistressstrain1.m:104:6:sr = evalexpr( fea.phys.css.eqn.vars{5,2}, [r;z], fea );
ex_axistressstrain1.m:105:6:st = evalexpr( fea.phys.css.eqn.vars{6,2}, [r;z], fea );
ex_axistressstrain1.m:106:6:sz = evalexpr( fea.phys.css.eqn.vars{7,2}, [r;z], fea );
ex_axistressstrain2.m:92:5:u = evalexpr( 'r*u', [r;z], fea );
ex_axistressstrain3.m:107:7:u_r = evalexpr( 'r*u', fea.grid.p, fea );
ex_axistressstrain3.m:108:7:u_z = evalexpr( 'w', fea.grid.p, fea );
ex_axistressstrain3.m:109:11:u_ref_r = evalexpr( u_ref_r, fea.grid.p, fea );
ex_axistressstrain3.m:110:11:u_ref_z = evalexpr( u_ref_z, fea.grid.p, fea );
ex_axistressstrain4.m:150:11:    T_i = evalexpr( 'T-273.15', rz, fea );
ex_axistressstrain4.m:157:12:    sr_i = evalexpr( ['(',sr,')*1e-6'], rz, fea );
ex_axistressstrain4.m:164:12:    st_i = evalexpr( ['(',st,')*1e-6'], rz, fea );
ex_axistressstrain4.m:171:13:    svm_i = evalexpr( ['(',svm,')*1e-6'], rz, fea );
ex_axistressstrain4.m:199:7:  T = evalexpr( 'T-273.15', [r;zeros(size(r))], fea );
ex_brinkman1.m:83:8:u_ns = evalexpr( 'sqrt(u^2+v^2)', [x;y], fea );
ex_brinkman1.m:84:8:u_br = evalexpr( 'sqrt(u2^2+v2^2)', [x;y], fea );
ex_compressibleeuler1.m:78:5:r = evalexprp( fea.dvar{1}, fea );
ex_compressibleeuler1.m:79:5:u = evalexprp( fea.dvar{2}, fea );
ex_compressibleeuler1.m:80:5:p = evalexprp( fea.dvar{3}, fea );
ex_compressibleeuler2.m:115:5:r = evalexprp( fea.dvar{1}, fea );
ex_compressibleeuler2.m:116:5:u = evalexprp( fea.dvar{2}, fea );
ex_compressibleeuler2.m:117:5:v = evalexprp( fea.dvar{3}, fea );
ex_compressibleeuler2.m:118:5:p = evalexprp( fea.dvar{4}, fea );
ex_compressibleeuler2.m:119:9:r_ref = evalexprp( rref, fea );
ex_compressibleeuler2.m:120:9:u_ref = evalexprp( uref, fea );
ex_compressibleeuler2.m:121:9:v_ref = evalexprp( vref, fea );
ex_compressibleeuler2.m:122:9:p_ref = evalexprp( pref, fea );
ex_compressibleeuler3.m:119:5:r = evalexprp( fea.dvar{1}, fea );
ex_compressibleeuler3.m:120:5:u = evalexprp( fea.dvar{2}, fea );
ex_compressibleeuler3.m:121:5:v = evalexprp( fea.dvar{3}, fea );
ex_compressibleeuler3.m:122:5:p = evalexprp( fea.dvar{4}, fea );
ex_compressibleeuler3.m:123:9:r_ref = evalexprp( rref, fea );
ex_compressibleeuler3.m:124:9:u_ref = evalexprp( uref, fea );
ex_compressibleeuler3.m:125:9:v_ref = evalexprp( vref, fea );
ex_compressibleeuler3.m:126:9:p_ref = evalexprp( pref, fea );
ex_compressibleeuler6.m:115:15:out.err = abs(evalexpr('sqrt(u^2+v^2)/sqrt(ga_ee*p/rho)',[1.9;0.4],fea) - 1.873526) / 1.873526;
ex_convdiff1.m:127:7:err = evalexpr0(s_err,xi,1,1:size(fea.grid.c,2),[],fea);
ex_convdiff1.m:128:7:ref = evalexpr0('c',xi,1,1:size(fea.grid.c,2),[],fea);
ex_convdiff5.m:89:8:c0p8 = evalexpr( 'c', [x;y], fea );
ex_convdiff6.m:82:9:c     = evalexpr( 'c',    x, fea );
ex_convdiff6.m:83:9:c_ref = evalexpr( refsol, x, fea );
ex_custom_equation1.m:100:7:err = evalexpr( ['abs(',refsol,'-',u,')'], linspace(0,opt.len,10), fea );
ex_diffusion1.m:133:7:err = evalexpr0(s_err,xi,1,1:size(fea.grid.c,2),[],fea);
ex_diffusion1.m:134:7:ref = evalexpr0('c',xi,1,1:size(fea.grid.c,2),[],fea);
ex_euler_beam1.m:81:10:err_v  = evalexpr( 'abs(v-v_ref)', ...
ex_euler_beam2.m:85:10:err_v  = evalexpr( 'abs(v-q_eb*x^2*(6*L^2-4*L*x+x^2)/(24*E_eb*I_eb))', ...
ex_euler_beam2.m:87:10:err_th = evalexpr( 'abs(vx-q_eb*x*(3*L^2-3*L*x+x^2)/(6*E_eb*I_eb))', ...
ex_euler_beam2.m:89:10:err_M  = evalexpr( 'abs(vxx-q_eb/2*(L-x)^2/(E_eb*I_eb))', ...
ex_fluidstructure1.m:101:8:ux_A = evalexpr( 'dx', p_Ai, fea );
ex_fluidstructure1.m:102:8:uy_A = evalexpr( 'dy', p_Ai, fea );
ex_fluidstructure1.m:121:16:[~,ind_gdof] = evalexprdof(0,1,fea,i_int);
ex_fluidstructure2.m:105:17:  ux_A(i_cnt) = evalexpr( 'dx', p_Ai, fea, i );
ex_fluidstructure2.m:106:17:  uy_A(i_cnt) = evalexpr( 'dy', p_Ai, fea, i );
ex_heattransfer1.m:124:10:T2_sol = evalexpr( 'T', [0.01;0.01], fea );
ex_heattransfer1.m:126:10:T5_sol = evalexpr( 'T', [0.01;0.005], fea );
ex_heattransfer1.m:128:10:T8_sol = evalexpr( 'T', [0.01;0], fea );
ex_heattransfer10.m:102:12:out.val = [evalexpr('u',[1;0.75],fea), ...
ex_heattransfer10.m:103:12:           evalexpr('T',[1;0.75],fea), ...
ex_heattransfer10.m:104:12:           evalexpr('T',[1;0.5],fea)];
ex_heattransfer2.m:104:9:T_sol = evalexpr( 'T', 0.1, fea );
ex_heattransfer3.m:95:15:    T(isol) = evalexpr( 'T', 0.02, fea, isol );
ex_heattransfer3.m:105:9:T_sol = evalexpr( 'T', 0.02, fea );
ex_heattransfer4.m:127:9:T_sol = evalexpr( 'T', [0.6;0.2], fea );
ex_heattransfer6.m:104:9:T_sol = evalexpr( 'T', [0.04;0.04], fea );
ex_heattransfer7.m:98:9:T_sol = evalexpr( 'T', fea.grid.p, fea );
ex_heattransfer8.m:132:9:T_sol = evalexprp( 'T', fea );
ex_heattransfer9.m:110:9:T_sol = evalexpr( 'T', x, fea );
ex_laplace1.m:112:7:err = evalexpr0(s_err,xi,1,1:size(fea.grid.c,2),[],fea);
ex_laplace1.m:113:7:ref = evalexpr0('u',xi,1,1:size(fea.grid.c,2),[],fea);
ex_laplace2.m:108:7:err = evalexpr0(s_err,xi,1,1:size(fea.grid.c,2),[],fea);
ex_laplace2.m:109:7:ref = evalexpr0('u',xi,1,1:size(fea.grid.c,2),[],fea);
ex_linearelasticity1.m:106:6:ui = evalexpr( fea.dvar{opt.idir}, p, fea );
ex_linearelasticity1.m:112:28:  out.serr(i) = norm( abs( evalexpr( fea.phys.el.eqn.vars{5+i, end}, p, fea ) - s*(i==opt.idir) ) );
ex_linearelasticity1.m:113:28:  out.eerr(i) = norm( abs( evalexpr( fea.phys.el.eqn.vars{14+i,end}, p, fea ) - s*(i==opt.idir) + s*0.3*(i<=3 & i~=opt.idir)) ) ;
ex_linearelasticity1.m:115:31:    out.pserr(i) = norm( abs( evalexpr( fea.phys.el.eqn.vars{11+i,end}, p, fea ) - (i==1) ) );
ex_linearelasticity1.m:116:31:    out.peerr(i) = norm( abs( evalexpr( fea.phys.el.eqn.vars{20+i,end}, p, fea ) - (i==1) + 0.3*(i~=1) ) );
ex_linearelasticity1.m:119:34:out.serr = [ out.serr norm( abs( evalexpr( fea.phys.el.eqn.vars{1, end}, p, fea ) - 1 ) ) ];
ex_linearelasticity2.m:116:22:    dp(i,:) = DSCALE*evalexpr( fea.dvar{i}, fea.grid.p, fea );
ex_linearelasticity3.m:96:17:    vm_stress = evalexpr( s_vm, fea.grid.p, fea );
ex_linearelasticity4.m:93:22:    dp(i,:) = DSCALE*evalexpr( fea.dvar{i}, fea.grid.p, fea );
ex_linearelasticity4.m:113:7:svm = evalexpr( fea.phys.el.eqn.vars{1,2}, fea.grid.p, fea );
ex_linearelasticity6.m:110:9:ps1_E = evalexpr( fea.phys.el.eqn.vars{12,2}, p_E, fea );
ex_linearelasticity6.m:111:9:ps2_E = evalexpr( fea.phys.el.eqn.vars{13,2}, p_E, fea );
ex_linearelasticity6.m:112:9:ps3_E = evalexpr( fea.phys.el.eqn.vars{14,2}, p_E, fea );
ex_linearelasticity6.m:115:11:out.w_E = evalexpr( 'w', p_E, fea );
ex_natural_convection.m:193:12:  u_eval = evalexpr( 'u', [x_mid; x_eval], fea );
ex_natural_convection.m:197:12:  v_eval = evalexpr( 'v', [x_eval; x_mid], fea );
ex_navierstokes1.m:202:14:c_ind = find(evalexpr0(s_len,xi,1,1:size(fea.grid.c,2),[],fea))';
ex_navierstokes1.m:203:7:err = evalexpr0(s_err,xi,1,c_ind,[],fea);
ex_navierstokes1.m:204:7:ref = evalexpr0(['sqrt((',s_refsol,')^2)'],xi,1,c_ind,[],fea);
ex_navierstokes10.m:94:5:u = evalexpr( 'u', p, fea );
ex_navierstokes11.m:86:5:u = evalexpr( 'u', [0.5;0.5;0.5], fea );
ex_navierstokes13.m:134:9:dp    = evalexpr('p',[0.45 0.55;0.205 0.205;0.21 0.21],fea);
ex_navierstokes14.m:102:5:u = evalexpr( s_velm, p, fea );
ex_navierstokes14.m:103:9:u_ref = evalexpr( s_refsol, p, fea );
ex_navierstokes14.m:161:12:  y_i(i) = evalexpr0( 'y', bdrm(6:end,ix), [], bdrm(1,ix), bdrm(2,ix), prob );
ex_navierstokes14.m:171:9:  y_j = evalexpr0( 'y', bdrm(6:end,ix), [], bdrm(1,ix), bdrm(2,ix), prob );
ex_navierstokes15.m:107:5:u = evalexpr( s_velm, p, fea );
ex_navierstokes15.m:108:9:u_ref = evalexpr( s_refsol, p, fea );
ex_navierstokes15.m:166:12:  y_i(i) = evalexpr0( 'y', bdrm(6:end,ix), [], bdrm(1,ix), bdrm(2,ix), prob );
ex_navierstokes15.m:176:9:  y_j = evalexpr0( 'y', bdrm(6:end,ix), [], bdrm(1,ix), bdrm(2,ix), prob );
ex_navierstokes16.m:117:16:[~,ind_gdof] = evalexprdof(0,1,fea,i_int);
ex_navierstokes17.m:112:5:u = evalexpr( 'u', [x;y_ref], fea );
ex_navierstokes1b.m:128:9:  err = evalexprc( s_err, ind_c, fea );
ex_navierstokes1b.m:129:9:  ref = evalexprc( ['sqrt((',fea.refsol,')^2)'], ind_c, fea );
ex_navierstokes1b.m:135:9:  err = evalexprp( s_err, fea, 1, ind_p );
ex_navierstokes1b.m:136:9:  ref = evalexprp( ['sqrt((',fea.refsol,')^2)'], fea, 1, ind_p );
ex_navierstokes2.m:191:12:vort     = evalexpr('vx-uy',[0.53;0.564],fea);
ex_navierstokes2b.m:119:8:vort = evalexpr( 'vx-uy', [0.53;0.564], fea );
ex_navierstokes3.m:183:9:dp    = evalexpr('p',[0.15 0.25;0.2 0.2],fea);
ex_navierstokes3b.m:159:6:dp = evalexpr('p',[0.15 0.25;0.2 0.2],fea);
ex_navierstokes5.m:123:9:  u_i = evalexpr( 'u', fea.grid.p, fea, i_sol );
ex_navierstokes5.m:124:9:  v_i = evalexpr( 'v', fea.grid.p, fea, i_sol );
ex_navierstokes5.m:125:9:  p_i = evalexpr( 'p', fea.grid.p, fea, i_sol );
ex_navierstokes6.m:346:14:    p_i(1) = evalexpr('p',[x;0.2],fea);
ex_navierstokes6.m:351:14:    p_i(2) = evalexpr('p',[x;0.2],fea);
ex_navierstokes8.m:105:5:U = evalexpr( 'sqrt(u^2+w^2)', [r;z], fea )';
ex_navierstokes8b.m:134:9:  err = evalexprc( s_err, ind_c, fea );
ex_navierstokes8b.m:135:9:  ref = evalexprc( ['sqrt((',fea.refsol,')^2)'], ind_c, fea );
ex_navierstokes8b.m:141:9:  err = evalexprp( s_err, fea, 1, ind_p );
ex_navierstokes8b.m:142:9:  ref = evalexprp( ['sqrt((',fea.refsol,')^2)'], fea, 1, ind_p );
ex_navierstokes9.m:113:5:u = evalexpr( 'u', fea.grid.p, fea );
ex_navierstokes9.m:114:5:w = evalexpr( 'w', fea.grid.p, fea );
ex_nonlinear_pde1.m:99:7:err = evalexpr0( 'abs(u_ref-u)', xi, 1, 1:size(fea.grid.c,2), [], fea );
ex_nonlinear_pde1.m:100:7:ref = evalexpr0( 'u',            xi, 1, 1:size(fea.grid.c,2), [], fea );
ex_nonlinear_pde2.m:87:11:  u_ref = evalexprp( 'u_ref', fea );
ex_nonlinear_pde2.m:94:7:err = evalexprp( 'abs(u_ref-u)', fea );
ex_nonlinear_pde2.m:95:7:ref = evalexprp( 'u',            fea );
ex_periodic2.m:62:6:ul = evalexpr( 'u', [zeros(1,100);y], fea );
ex_periodic2.m:63:6:ur = evalexpr( 'u', [ones(1,100);y],  fea );
ex_periodic2.m:126:14:    y_i(k) = evalexpr0( 'y', xii(:,k)', [], indc(k), inde(k), prob );
ex_periodic2.m:143:9:    y = evalexpr0( 'y', xi', [], indc, inde, prob );
ex_piezoelectric1.m:213:17:  up1  = DSCALE*evalexpr( 'u', p1b, fea );
ex_piezoelectric1.m:214:17:  vp1  = DSCALE*evalexpr( 'v', p1b, fea );
ex_piezoelectric1.m:215:17:  up2  = DSCALE*evalexpr( 'u', p2b, fea );
ex_piezoelectric1.m:216:17:  vp2  = DSCALE*evalexpr( 'v', p2b, fea );
ex_planestrain1.m:91:12:v_disp   = evalexpr( s_disp, [100e-3 120e-3-2*sqrt(eps);0 0]+sqrt(eps), fea )';
ex_nonnewtonian1.m:113:5:u = evalexpr( s_velm, p, fea );
ex_nonnewtonian1.m:114:9:u_ref = evalexpr( s_refsol, p, fea );
ex_planestrain2.m:136:8:u    = evalexpr( 'u', p, fea ).';
ex_planestrain2.m:137:8:src  = evalexpr( s_sx, p, fea ).';
ex_planestrain2.m:138:8:sthc = evalexpr( s_sy, p, fea ).';
ex_planestrain2.m:139:8:szc  = evalexpr( s_sz, p, fea ).';
ex_planestrain2.m:147:8:v    = evalexpr( 'v', p, fea ).';
ex_planestrain2.m:148:8:src  = evalexpr( s_sy, p, fea ).';
ex_planestrain2.m:149:8:sthc = evalexpr( s_sx, p, fea ).';
ex_planestrain2.m:150:8:szc  = evalexpr( s_sz, p, fea ).';
ex_planestress3.m:127:8:s_02 = evalexpr( s_expr, [0;2], fea );
ex_planestress2.m:107:7:sm  = evalexpr( s_vm, [0.5;0.5], fea );
ex_planestress2.m:108:7:s01 = evalexpr( s_vm, [dtol;1],    fea );
ex_planestress2.m:109:7:s10 = evalexpr( s_vm, [1;dtol],    fea );
ex_planestress2.m:110:7:s00 = evalexpr( s_vm, [dtol;dtol], fea );
ex_planestress2.m:111:7:s11 = evalexpr( s_vm, [1;1],       fea );
ex_planestress4.m:164:12:sy_D     = evalexpr( s_sy, [1e-3;1e-6], fea );
ex_planestress5.m:111:12:sy_D     = evalexpr( s_sy, [2;0]+sqrt(eps)*1e1, fea );
ex_planestress6.m:91:12:v_disp   = evalexpr( s_disp, [100e-3 120e-3-2*sqrt(eps);0 0]+sqrt(eps), fea )';
ex_poisson2.m:131:7:err = evalexpr0(s_err,xi,1,1:size(fea.grid.c,2),[],fea);
ex_poisson2.m:132:7:ref = evalexpr0('u',xi,1,1:size(fea.grid.c,2),[],fea);
ex_poisson1.m:176:7:  u = evalexpr( 'u', x, fea )';
ex_poisson1.m:198:7:err = evalexpr0(s_err,xi,1,1:size(fea.grid.c,2),[],fea);
ex_poisson1.m:199:7:ref = evalexpr0('u',xi,1,1:size(fea.grid.c,2),[],fea);
ex_poisson3.m:113:7:  u = evalexpr( 'u', g.p, fea );
ex_poisson3.m:129:5:u = evalexpr( 'u', [x(:) y(:)]', fea );
ex_poisson4.m:123:7:err = evalexpr0(s_err,xi,1,1:size(fea.grid.c,2),[],fea);
ex_poisson4.m:124:7:ref = evalexpr0('u',xi,1,1:size(fea.grid.c,2),[],fea);
ex_poisson5.m:109:7:err = evalexpr0(s_err,xi,1,1:size(fea.grid.c,2),[],fea);
ex_poisson5.m:110:7:ref = evalexpr0('u',xi,1,1:size(fea.grid.c,2),[],fea);
ex_poisson6.m:109:5:u = evalexpr( 'u', [x(:) y(:) z(:)]', fea );
ex_poisson7.m:126:7:err = evalexpr0(s_err,xi,1,1:size(fea.grid.c,2),[],fea);
ex_poisson7.m:127:7:ref = evalexpr0('u',xi,1,1:size(fea.grid.c,2),[],fea);
ex_potential_flow1.m:72:12:U_T = sqrt(evalexpr( 'psix^2+psiy^2', p_T, fea ));
ex_potential_flow1.m:186:9:  cp  = evalexpr( 'cp', p_bdr, fea );
ex_resistive_heating1.m:172:65:% vector stored in prob.expr{ u_V }. Expected to be called from evalexpr0.
ex_resistive_heating1.m:177:49:  % Extract variable from the calling function, evalexpr0.
ex_resistive_heating1.m:206:7:  Q = evalexpr0( s_sigma, xi, ind_s, ind_c, [], prob, aJac ).*( Vx.^2 + Vy.^2 + Vz.^2 );
ex_robinbc1.m:67:7:err = evalexpr0(s_err,xi,1,1:size(fea.grid.c,2),[],fea);
ex_robinbc1.m:68:7:ref = evalexpr0('u',xi,1,1:size(fea.grid.c,2),[],fea);
ex_spanner.m:95:22:    dp(i,:) = DSCALE*evalexpr( fea.dvar{i}, fea.grid.p, fea );
ex_swirl_flow1.m:124:10:  v_th = evalexpr( 'v', [r;zeros(1,length(r))], fea );
ex_swirl_flow1.m:143:8:v_th = evalexpr( 'v', [r;zeros(1,length(r))], fea )';
ex_swirl_flow3.m:204:7:  u = evalexpr( 'u', pa, fea, i );
ex_swirl_flow3.m:205:7:  v = evalexpr( 'v', pa, fea, i );
ex_swirl_flow3.m:206:7:  w = evalexpr( 'w', pa, fea, i );
ex_swirl_flow3.m:248:12:  x_i(i) = evalexpr0( 'r', bdrm(6:end,ix), [], bdrm(1,ix), bdrm(2,ix), prob );
ex_swirl_flow3.m:258:9:  x_j = evalexpr0( 'r', bdrm(6:end,ix), [], bdrm(1,ix), bdrm(2,ix), prob );
ex_waveequation1.m:150:15:    u(isol) = evalexpr( 'u', xp, fea, isol );
ex_waveequation1.m:161:25:out.err  = abs( u_ref - evalexpr( 'u', xp, fea, isol ) )/abs(u_ref);