Artificial Stabilization with Navier Stokes Equations

Hello, I am looking to implement a boundary observer in a simulation based on the navier stokes equations. As a result, I am looking to implement custom PDE equations to be simulated. I am more experienced in control, and am rather new to PDE simulations and FEA multiphysics. Now, my first thought was to introduce additional observer equations alongside the navier stokes equations, this would require introducing additional dependent variables which does not seem to be possible:



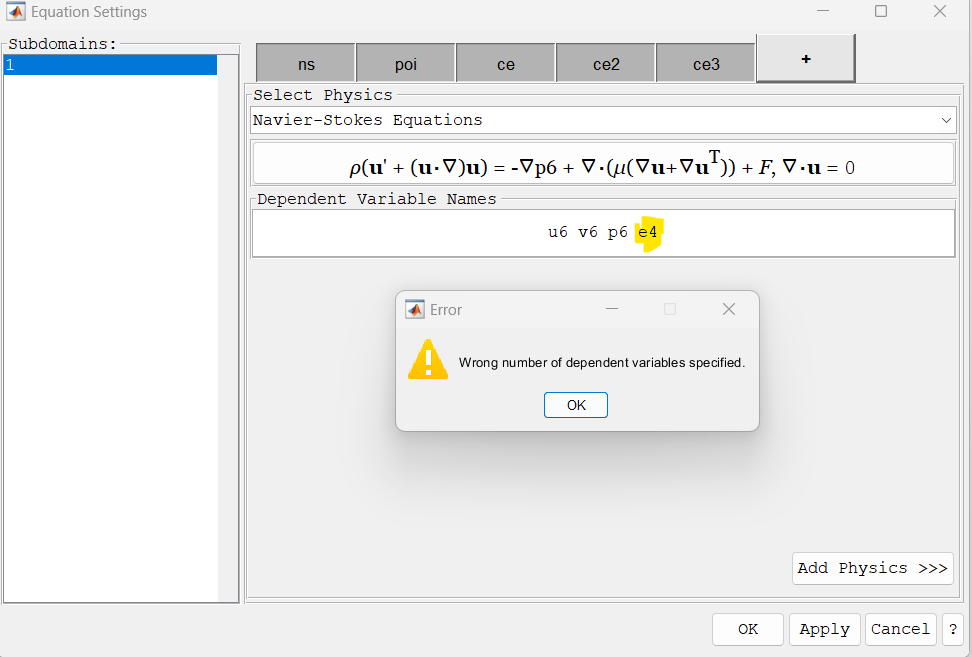the extra variable is not acceptable. I next tried to recreate everything as a customized PDE and simulate it that way. I first simulated the navier stokes equations through the standard module provided by FEA multiphysics over an airfoil, using laminar flow (to simplify things), and the results are fairly satisfactory: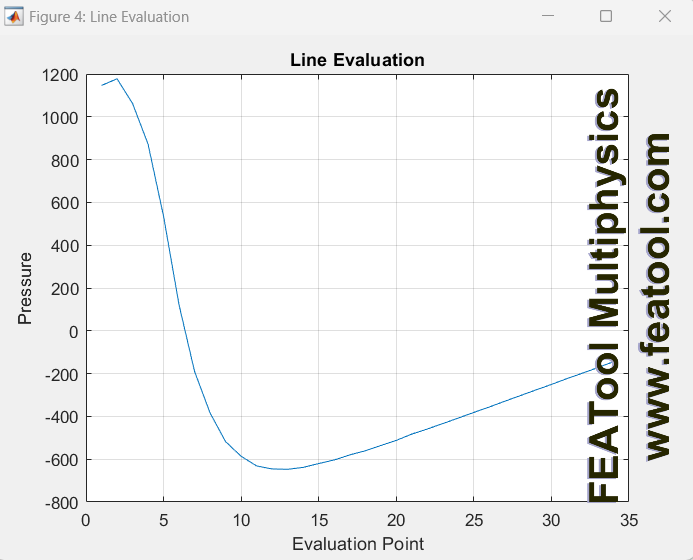




you can see the pressure along one of the airfoils surface above. I then tried to recreate these results with a customized PDE:



Unfortunately, the solver (I used backslash here as mumps could not reach a solution at all) did not like this as seen: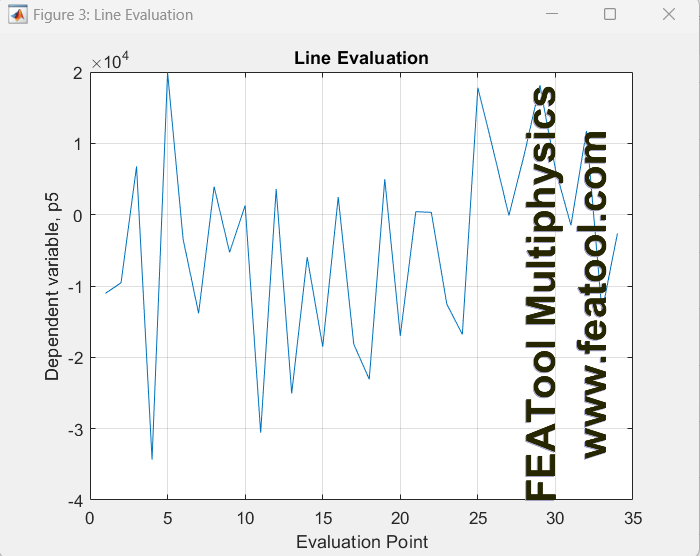





It appears to be a stability issue with pressure. From reading documentation, this seems to be a result from the difficulty in satisfying the continuity equation with low order finite elements or non-conforming grids. It appears the navier stokes module handles this with a pressure artificial stabilization algorithm. I am fairly inexperienced with these solver methods, is this something I could easily replicate in the custom PDE equation solver? And if so, how would I do this?

Is it accomplished by adding an artificial viscosity term (mu_s) to (mu + mu_s) in the custom navier stokes equations? Maybe I can extract this value after using the original navier stokes module? Any advice on moving forward would be greatly appreciated.

Hi Sean,

Thank you for trying the software and clear description of the issue.

As for the Navier-Stokes equations, if you use 1:st order approximations (finite element shape/basis functions) for both the pressure and velocity the solution will not be stable as you have found out. To handle this the Navier-Stokes physics mode has implemented pressure stabilization PSPG which you can find by clicking on the "Artificial Stabilization" button on the "ns" tab in the "Equation Settings" dialog box (https://www.featool.com/doc/physics#phys_artstab). Unfortunately this expression is rather elaborate and will be computed and added automatically before solving, so it doesn't show up inspecting the equation. In general the contribution to the pressure/continuity equation will look like

pspg = [stab_coef,'/sqrt( ',(u^2+v^2),'/h_grid^2 + 4*1/dt^2 + 9*(',miu,'/',rho,')^2/h_grid^4 + eps )/',rho,'*(',s_eqn,')'];

% where s_eqn is the combined momentum (velocity) equation strings

Alternatively, the easier way is to simply use 2nd or higher approximations for the velocities (P2/P1) shape functions and this problem goes away automatically, however it comes with higher cost of course as it requires more degrees of freedom for the velocities.

That said, although I'm not quite familiar with observer equations I think you should be able to just keep the Navier-Stokes physics mode as is (using the PSPG stabilization). And just add a new custom equation with one dependent variable for the observer equation. Even if they are not defined in the same physics mode you can still couple and use them freely in all physics mode/equations.

I hope this helps to clarify some things.

Hello,

Thank you for the quick and informed response. I am assuming the only step needed for higher order approximations is changing this setting: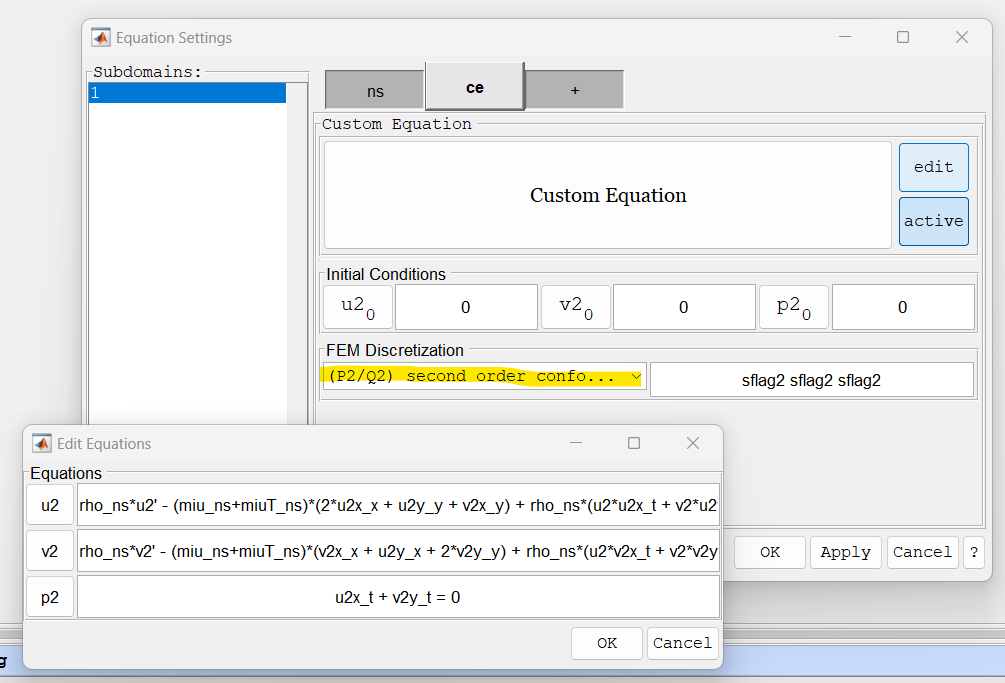



I tried this before and it did not improve the results much. However, I am thinking it is likely how I am setting the boundary conditions which may be the issue. The boundary conditions are defined as: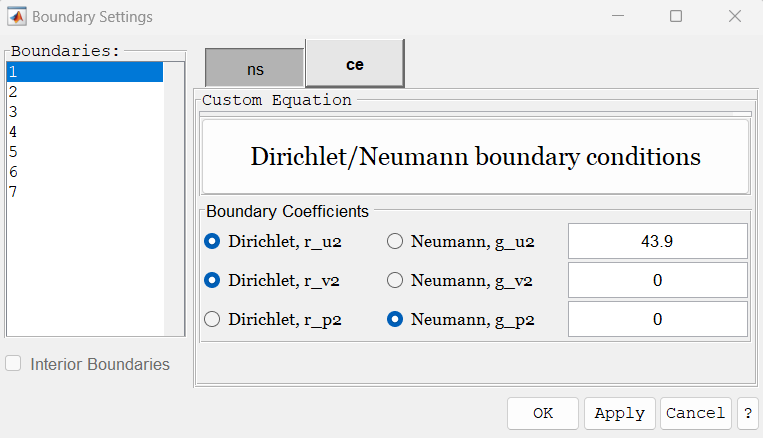




With the standard navier stokes physics, I set as
1) constant velocity in x direction, zero velocity in y direction
2) constant pressure of 0
3) constant velocity in x direction, zero velocity in y direction
4) constant velocity in x direction, zero velocity in y direction
5) constant velocity in x direction, zero velocity in y direction
6) no slip wall
7) no slip wall

where (6) and (7) are the surfaces of the airfoil. These settings gave me good results. This is what I put for the custom PDE boundary condition settings (trying to replicate the above ones)

1) Dirichlet u2 = constant vel, Dirichlet v2 = 0, Neumann p2 = 0 (g=0)
2) Dirichlet u2 = u2, Dirichlet v2 = v2, Dirichlet p2 = 0
3) Dirichlet u2 = constant vel, Dirichlet v2 = 0, Neumann p2 = 0 (g=0)
4) Dirichlet u2 = constant vel, Dirichlet v2 = 0, Neumann p2 = 0 (g=0)
5) Dirichlet u2 = constant vel, Dirichlet v2 = 0, Neumann p2 = 0 (g=0)
6) Dirichlet u2 = 0, Dirichlet v2 = 0, Neumann p2 = 0 (g=0)
7) Dirichlet u2 = 0, Dirichlet v2 = 0, Neumann p2 = 0 (g=0)

I am a bit unsure of the boundary conditions settings, I have tried many variations other then these but have had no success.

If it is not the boundary conditions settings, then I am not sure what it could be. Lastly, yes I can create the observer equations as custom ones, I just need to get this stability issue figured out first.

Thanks, Sean

I see, ok for the outflow boundary (2) either you typically would have zero (constant) pressure:

  Neumann u2 = 0, Neumann v2 = 0, Dirichlet p2 = 0

or a completely free (Neutral) condition

  Neumann u2 = 0, Neumann v2 = 0, Neumann p2 = 0

Specifying all "u,v,p" on the same boundary is not very typical and would be a very unusual boundary condition.

Thank you, I initially tried the first boundary conditions you suggested and the results were all over the place. I tried it again today, and the pressure is somewhat better but still unstable. The velocity solved pretty well, however this is what the pressure along the edge of the airfoil looks like:



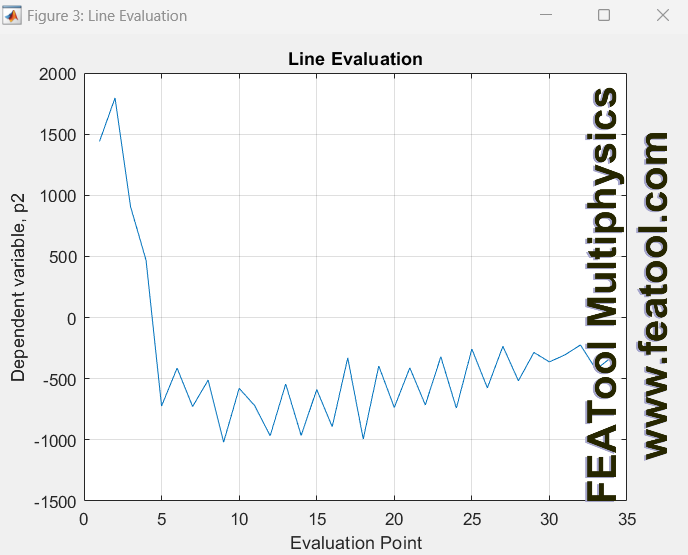From what I see, this does not appear to be a boundary condition problem but rather the handling of turbulence with a laminar solver. I re-tried the simulation today with a laminar solver on the standard navier stokes physics module and it was running into some numerical instability on the pressure as well. I then implemented the algebraic turbulence model, and this eliminated the instability in the solver. This is what the pressure should look like:



Anyhow it is very finicky. I am not sure if I can implement the algebraic turbulence model manually in the custom equation version?

I will lower the inlet velocity and maybe make a finer mesh for now to see if I can get stable results. In the future I will need to compare with openfoam RANS equations, so ill have to figure out how to integrate custom observer equations into that.

Hmm, kind of hard to say where the issue might be. The algebraic turbulence model is very easy to add though:

miu := miu + miu_T
wall_bdr = [<array with wall boundaries>]
miu_T =  rho_ns*turbulent_mixing_length(prob,0.41,0.09,wall_bdr,x,y)^2*sqrt((uy+vx)^2)

where the turbulent mixing length is given by the function

https://www.featool.com/doc/turbulent__mixing__length_8m

EDIT: Also see here for more on the algebraic turbulence model https://www.featool.com/tutorials/2020/01/08/2020-01-08-Implementation-of-an-Algebraic-Turbulence-Model

Dear Sean,

Please find some answers to your questions below. I think one of the big issues is if you want to simulate full 3D and/or turbulent flow?  In that case the built-in solver will likely not be efficient enough and you would have to use the OpenFOAM or SU2 solvers. In that case the equations and "observer" cannot be changed/used as the solvers are already compiled and can only be used "as is".

Sean_Smith wrote

I was able to get the results slightly better with a finer mesh however the pressure response is still jittery with some instability.

I have a few more questions that are not so much related to my forum post, but pertain to if achieving my end goal is possible with this simulation framework. So my end goal is to design a boundary observer based on the navier stokes equations, and a limited number of pressure measurements, to estimate the force on the surface of a sail (represented as an airfoil for now to simplify things).

The limited number of pressure measurement observer design will require further theoretical development on my side, so for now I will consider all pressure is available for feedback. A simple observer design can be considered:

'Navier Stokes equation' = k(p-p_hat)

Where p is the measured or real pressure and p_hat is the estimated value from the observer. So, to simulate the observer, I need to have the steady state solution of a simulation available at each iteration. So my question is:

1) I can simulate the NS equation side by side with my observer, but I imagine the observer wont be using the steady state solution values from the NS equation (it will be using the non-converged solution?), I apologize for my limited simulation knowledge. Is it possible to solve the problem with the NS equations, then export the solution data, and re run the simulation with the observer while implementing the exported solved data, for p, at each iteration of the new simulation?

It is not quite clear to be if the observer should actually modify the equation/physics. If not it is probably not a good idea to use a custom function approach, that is make a custom function "function p_hat(p,x,y)" that returns all zeros, but gives you the pressure in each solution step to export and use. See for example here

https://www.featool.com/doc/physics#phys_coef_user

Sean_Smith wrote

2) My next question is, can I implement the observer solver on a limited domain around the airfoil? Different from the initially defined domain, but also does not interfere with the currently defined geometry.

Technically it should be possible to define a region for which a function is non-zero, the easiest would be if you have defined a boundary segment apriori so you can just use that segment for your observer.

Sean_Smith wrote

3) I will eventually want to simulate a dynamic problem (not stationary anymore), where the airfoils angle of attack changes dynamically. I was thinking, the best way to implement this is have the inflow velocity change its angle, as a function of time, over the course of the simulation? Or would you recommend another way to consider this?

Yes, changing the direction of the inflow in an otherwise circular domain would probably be the best approach for FEATool as moving boundaries are yet not very robust.

Sean_Smith wrote

My biggest concern is question 1, because when I reach the stage of limited sensor measurements, I will want to run the observer with only a limited amount of pressures available for feedback (sensors), at specific locations, for the observer.

Lastly, the NS equations defined in the NS physics module are derived in the 'weak' form, including test functions, to solve with the FEM approach? I may look to simulate the linearized NS equations/linear observers and understanding this implementation is important.

Thanks, Sean

Yes, the built-in multiphysics solver employs a finite element discretization with the weak formulation. If you just want to solve linear Stokes flow you can simply remove the non-linear terms from the momentum equations ("u*ux + v*uy" etc). In contrast the external OpenFOAM and SU2 CFD solvers use the Finite Volume method for discretization.

I hope this helps somewhat.

With reference to your first answer, I am not sure exactly what you are saying. However, I will set the question up this way which similar to what I want. Lets say I am simulating the navier stokes equations on this airfoil problem, and I want a, external force along the airfoil boundary which varies with position. And lets say I have this force represented in a file of data at each point. I am still inexperienced with how the solver works, but if I create an m-script function called "force(x,y,p), as you said with:

https://www.featool.com/doc/physics#phys_coef_user

and if I reference this force function as an expression in a constants module, within the equation settings, then use this constant expression in the force definition within the navier stokes equation, can I introduce a non zero force into the navier stokes equation when it evaluates along the surface of the airfoil? Does the solver iteratively enter the force function when it is solving? And with the force data file, can I just define values along the surface of the airfoil or do I need to define values within the entire domain (unsure with what it would be expecting in return). I am a little confused with the framework in how it would call the function.

So basically, for the built-in solvers you can enter and use any expressions in equation and boundary coefficients, be it constants, expressions, as described here https://featool.com/doc/physics#phys_coef, and that even extends to your own functions. So if  you define and use a function "force(x,y,p)" as a coefficient somewhere, the solver will first evaluate x, y, and p, and then try to call a function "force" with the arguments. The specified coordinates x, y, and p will be evaluated in the quadrature points and depends on where your function is called (boundary, subdomain etc). So your function will have to interpolate your data to x, and y, and return a corresponding results with the same dimensions/size as the inputs.

Some more references on this:

https://forum.featool.com/external-function-td644.html#a647

https://forum.featool.com/Use-of-Functions-as-Boundary-Conditions-td1061.html#a1062